Distributed systems offer fantastic gains when it comes to solving large-scale problems. By sharing the computation load, you can solve problems too large for a single computer to handle, or solve problems in a fraction of the time it would take with a single computer. Maple, together with the Maple Grid Computing Toolbox makes it easy to create and test parallel distributed programs.
Maple includes the ability to easily set up multi-process computations on a single computer. The Maple Grid Computing Toolbox extends this power to multi-machine or cluster parallelism. The two versions are fully compatible, so that an algorithm can be created and fully tested using the local implementation inside Maple, and then deployed to the full cluster using the toolbox, without changes to the algorithm.
Example: Monte Carlo Integration
Random values of x can be used to compute an approximation of a definite integral according to the following formula.
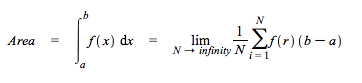
This procedure efficiently calculates a one-variable integral using the above formula where r is a random input to f.

A sample run using 1000 data points shows how this works:
![]()
This can be computed exactly in Maple to show the above approximation is rough, but close enough for some applications.

A parallel implementation adds the following code to split the problem over all available nodes and send the partial results back to node 0. Note that here the head node, 0, is used to accumulate the results, and does not actually do any computations.

Integrate over the range, lim, using N samples. Use as many nodes as are available in your cluster.
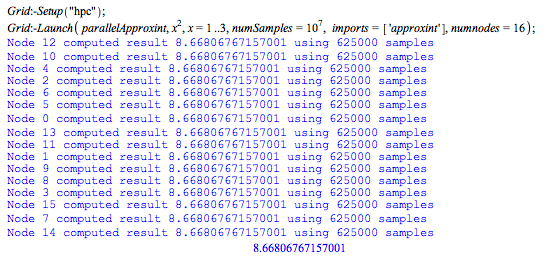
Execution times are summarized as follows. Computations were executed on a 3-blade cluster with 6 quad-core AMD Opteron 2378/2.4GHz processors and 8GB of memory per pair of CPUs, running Windows HPC Server 2008 and Maple 15.
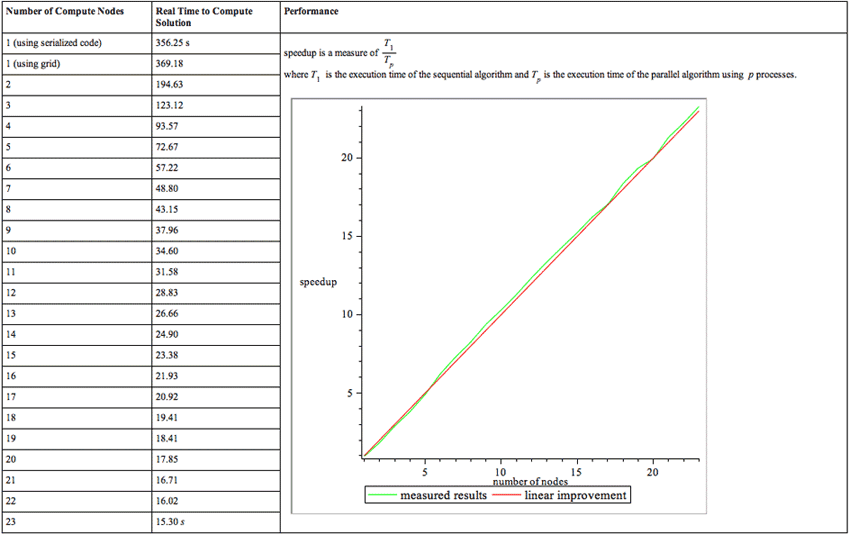
The first number in the table is the compute time in Maple, without using the Maple Grid Computing Toolbox (around 6 minutes). The rest of the times use the Maple Grid Computing Toolbox with a varying number of cores. The graph shows that adding cores scales linearly. When 23 cores are dedicated to the same example, it takes only 15.3 seconds to complete.