The Advantages of Symbolic Computation

MapleSim is the only comprehensive modeling system built within a natively symbolic framework and, as such, it avoids some of the worst sources of error and computational inefficiencies generated by traditional, numeric-based modeling tools. Symbolic computation is quickly becoming one of the most important and defining technologies of next generation modeling techniques. It provides the flexibility to develop model equations quickly and it offers the flexibility to better manage models and get to the optimal results faster.

Symbolic computation provides:

• Model equations in natural mathematical form
• Equation-based custom component development
• Symbolic model simplification and DAE reduction
• Optimized code generation

Model equations in natural mathematical form

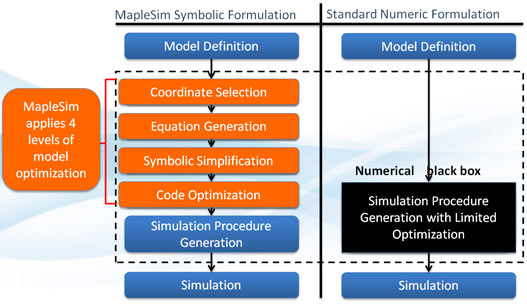
MapleSim is powered by a fully symbolic math engine that maintains the detailed mathematical structure of the model equations. In contrast, all other physical modeling and signal flow modeling systems are based on a purely numerical model formulation framework, which are essentially black boxes. With conventional systems, once you enter parameter values, procedures are generated internally for use by the solver routines, to work only with these specific values. Because these procedures do not maintain the mathematical structure of the equations, it becomes very difficult to enhance your model structure or systematically explore your parameter options. By contrast, the unique symbolic approach of MapleSim actually exposes and provides access to the model equations in very useful ways.

With MapleSim, you can see the model equations as differential equations, transfer functions, or in matrix form. Seeing the equations in familiar forms not only assists you in discerning the correctness of the models, but also helps you to communicate and share model information. Combined with the ability to attach live documents to your MapleSim model, you can view, record, and share your model, and all of the supporting details and analysis, in rich technical documents that are updated automatically when your model changes.

These equations can also be fully parametric, with design parameters left in symbolic form, to provide greater flexibility in analysis. You can easily manipulate and post-process equations for key analytical tasks including:

• Frequency analysis
• Sensitivity analysis
• Parameter exploration
• Linearization

Equation-based custom component development

In addition to its extensive collection of prebuilt modeling components, one of the unique features of MapleSim is the simplicity of its custom component creation. If you know the governing equations (differential, algebraic, DAE, or others), you can simply enter the equations in a natural way, and with the press of a button you can create a reusable and sharable component that you can include in your models. Users find the time savings and convenience of this approach to be invaluable as it avoids all of the time-consuming programming required by most systems. The time reduction can be as dramatic as days of programming versus minutes using a simple MapleSim template to create a new model component.

Situations where this capability is very useful include:

• Implementation of new models as presented in papers, reference books, or from your own research. In many cases, you can readily identify fully validated model equations for complex systems, but your modeling system has not caught up to the state of knowledge in your domain. When that happens, with other systems, you can choose to spend an inordinate amount of time converting the complex model equations into a form suitable for the system’s scripting language (possibly days of work); wait for your vendor to implement the model equation as a feature in a future version (the more specific your needs are, the less likely this will ever happen); or simply move on with an inadequate model. MapleSim provides a convenient alternative. If you know the equations, simply enter them into a MapleSim custom component template, just as they appear in your paper or research, and press a button.
• Application of industry-standard, pre-validated model definitions. Certain industries, such as automotive and aerospace, establish de facto standard definitions of components that have been validated over years of use and experience. This can happen at the company level (specific to your business, and possibly proprietary), or to an industry. Many engineers prefer their system models to use these accepted standard definitions. Using equation-based custom components in MapleSim, it is a very quick process to create components that use these definitions. With conventional systems, you are forced to deal with complex programming while trying to configure components to apply the standard equations within the black box framework. In that case, you cannot be completely certain that a component is faithful to the equations.

Specific applications include:

• Contact modeling
• Mean value engine models
• Battery modeling (electrical, thermal, chemical)
• Complex motors
• Non-ideal components

Symbolic model simplification and DAE reduction

In MapleSim, the unique symbolic model formulation framework generates model equations that are flexible and easy to work with. These equations are available to the user and are also used by MapleSim itself. One direct consequence is the ability of MapleSim to symbolically simplify the model equations with the goal of minimizing final computation time.

In all real-world modeling applications, the equations are formulated through some systematic process, whether it is manual derivation by an engineer or algorithmic generation by software. This process inevitably results in non-optimal equation sets, which can include redundant calculations, spurious equations not required for the simulation solution, and under-simplified expressions. With conventional modeling software, the algorithms that are typically deployed can only do limited simplification, due to the black box nature of the formulation. Once the equations are set up, you cannot change the algebraic structure. For example, if there is a simple instance of the formula , which through trigonometric identities always evaluates to 1, there is no way the software will identify this relationship. The solver will be forced to iteratively calculate all of the trig terms (very expensive calculations) over and over again through the iterations. Such terms are very common in application areas such as multibody dynamics, and in the end traditional solvers carry an extraordinary computation burden that adds nothing to the quality of the results.

MapleSim is smarter. Using advanced symbolic manipulation techniques, MapleSim can apply trig identities, look for term cancellations, pre-compute obvious terms such as multiplication with ones or zeroes, and, in general, manipulate the algebra to seek as many simplifications as possible. The results can provide a dramatic increase in speed over conventional modeling systems. In cases where systems are represented by differential-algebraic equations (DAEs), the symbolic routines in MapleSim can actually reduce the index of the DAEs to make a fast solution possible.

All of these techniques are lossless simplifications. In MapleSim, model simplification techniques produce more compact and efficient model equations with no loss of fidelity.

Optimized code generation

If the end goal of your modeling is hardware-in-the-loop (HIL) testing, MapleSim offers what is often the fastest real-time code for your plant models. In addition to the unique symbolic techniques that simplify the algebra of the model equations without reducing fidelity, the MapleSim code generation tools convert these equations to real-time source code while applying additional optimization steps that dramatically speed up real-time performance.

The optimizing tools extract common terms and replace them with a single variable whose value is computed in advance. During each iteration, all references to this term are determined simply by looking at the precomputed value, rather than recalculating the original mathematical expression each time. Removing expensive calculations from inside the iteration loops can decrease the number of calculations for that term alone from thousands to one in a typical application. When you combine the savings for all of the possible terms, and extend this basic technique to more complex algebraic constructs, the final computation time reduction can be substantial. All of this can only be achieved if the modeling tool has the symbolic and mathematical flexibility that MapleSim offers.

MapleSim provides tools to convert model equations to important target languages including C, MATLAB®, Java™, BASIC, and FORTRAN. With add-on connectivity toolboxes, the resulting code can easily be used as a foundation for real-time applications based on the Simulink® platform. For example, the MapleSim Connector delivers a complete S-function that you can immediately include in your Simulink® models.

The time savings resulting from MapleSim’s model equation formulation and automatic generation of real-time code blocks is substantial, and can literally reduce project time from months to days. This savings has become one of the most important reasons fueling the rapid adoption of MapleSim in numerous industries.

MapleSim replaces repeated calls to computationally expensive function calls and algebraic terms with precomputed single values, prior to the iteration.

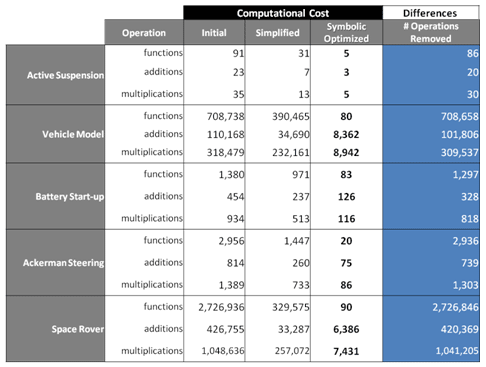As a result of its symbolic equation-formulation, simplification, and optimization technologies, MapleSim dramatically reduces the computational effort of simulation. With MapleSim, you do not have to choose between model fidelity and real-time performance.